In addition to CpG sites, there are 4 sets of genomic regions to be covered in the analysis. The table below gives a summary of these annotations.
| tiling |
n.a. |
129076 |
| genes |
n.a. |
29439 |
| promoters |
n.a. |
29526 |
| cpgislands |
n.a. |
25791 |
Region length distributions
The plots below show region size distributions for the region types above.
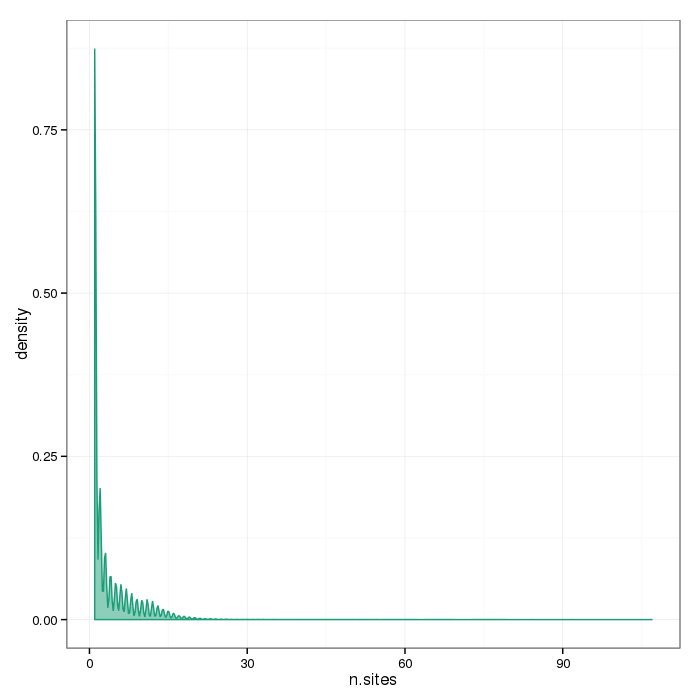
Number of sites per region
The plots below show the distributions of the number of sites per region type.
Dimension reduction is used to visually inspect the dataset for a strong signal in the methylation values that is related to samples' clinical or batch processing annotation. RnBeads implements two methods for dimension reduction - principal component analysis (PCA) and multidimensional scaling (MDS).
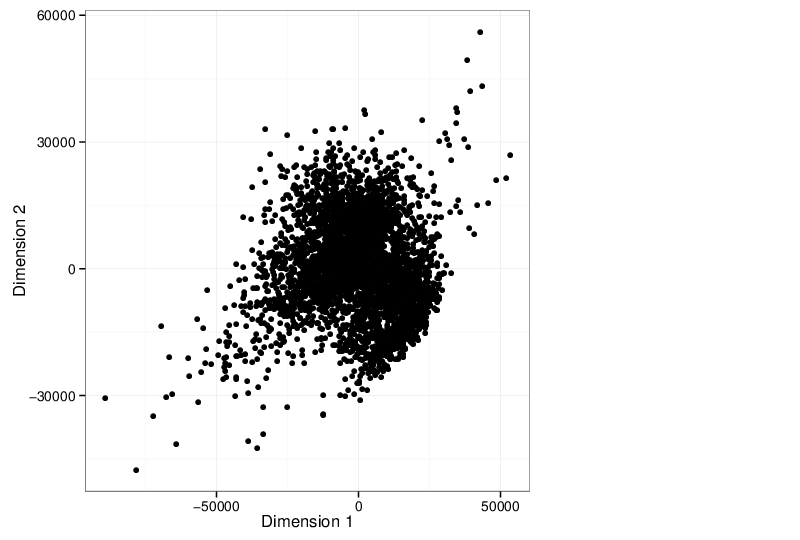
Multidimensional Scaling
The scatter plot below visualizes the samples transformed into a two-dimensional space using MDS.
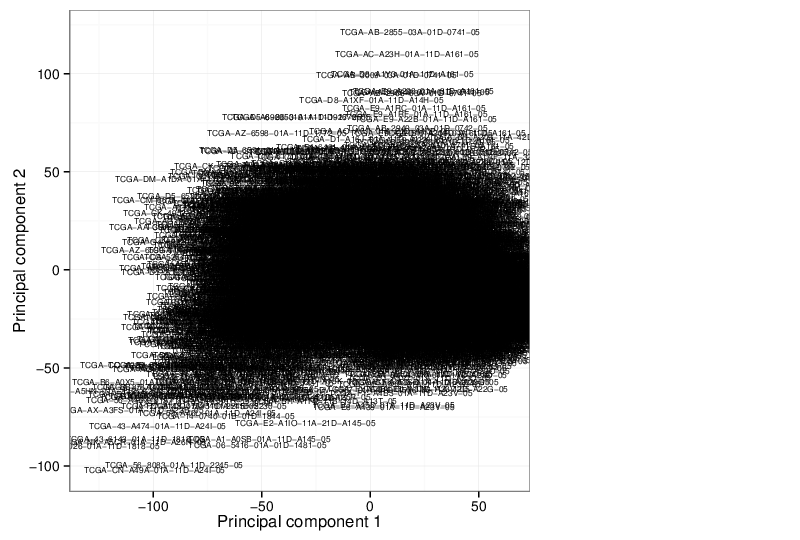
Principal Component Analysis
Similarly, the figure below shows the values of selected principal components in a scatter plot.
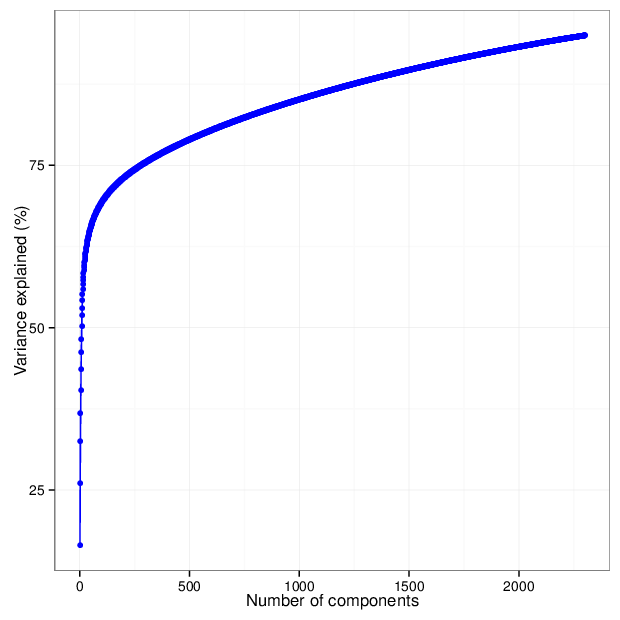
The figure below shows the cumulative distribution functions of variance explained by the principal components.
The table below gives for each location type a number of principal components that explain at least 95 percent of the total variance. The full tables of variances explained by all components are available in comma-separated values files accompanying this report.
| sites |
2300 |
csv |
| tiling |
2005 |
csv |
| genes |
1601 |
csv |
| promoters |
1679 |
csv |
| cpgislands |
1743 |
csv |
In this section, different properties of the dataset are tested for significant associations. The properties can include sample coordinates in the principal component space, phenotype traits and intensities of control probes. The tests used to calculate a p-value given two properties depend on the essence of the data:
- If both properties contain categorical data (e.g. tissue type and sample processing date), the test of choice is a two-sided Fisher's exact test.
- If both properties contain numerical data (e.g. coordinates in the first principal component and age of individual), the correlation coefficient between the traits is computed. A p-value is estimated using permutation tests with 10000 permutations.
- If property A is categorical and property B contains numeric data, p-value for association is calculated by comparing the values of B for the different categories in A. The test of choice is a two-sided Wilcoxon rank sum test (when A defines two categories) or a Kruskal-Wallis one-way analysis of variance (when A separates the samples into three or more categories).
Note that the p-values presented in this report are not corrected for multiple testing.
Associations between Principal Components and Traits
The computed sample coordinates in the principal component space were tested for association with the specified traits. Below is a list of the traits and the tests performed.
| Type |
Kruskal-Wallis |
| Study |
Kruskal-Wallis |
| Gender |
Wilcoxon |
| Days to birth |
Correlation |
| Vital status |
Wilcoxon |
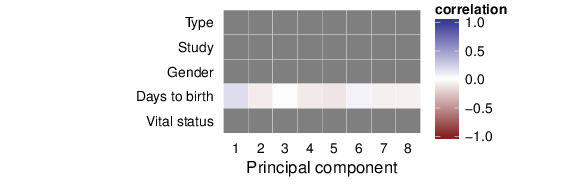
The next figure shows the computed correlations between the first 8 principal components and the sample traits.
The values presented in the figure above are avaialable in CSV (comma-separated value) files accompanying this report.
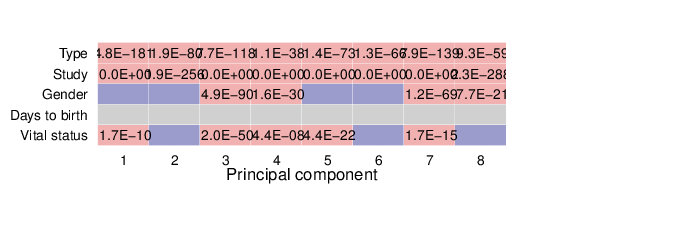
The heatmap below summarizes the results of permutation tests performed for associations. Significant p-values (values less than 0.01) are displayed in pink background.
The full tables of p-values for each location type are available in CSV (comma-separated value) files below.
Associations between Traits
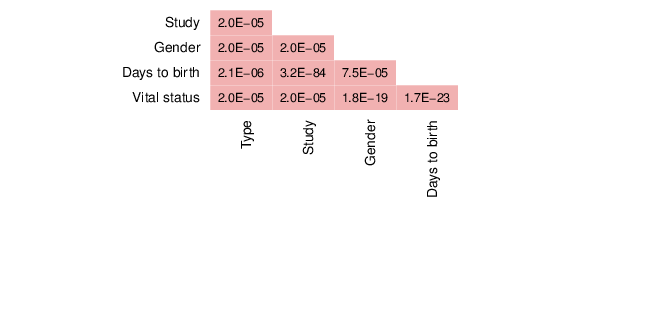
This section summarizes the associations between pairs of traits.
The figure below visualizes the tests that were performed on trait pairs based on the description provided above. In addition, the calculated p-values for associations between traits are shown. Significant p-values (values less than 0.01) are displayed in pink background. The full table of p-values is available in a dedicated file that accompanies this report.
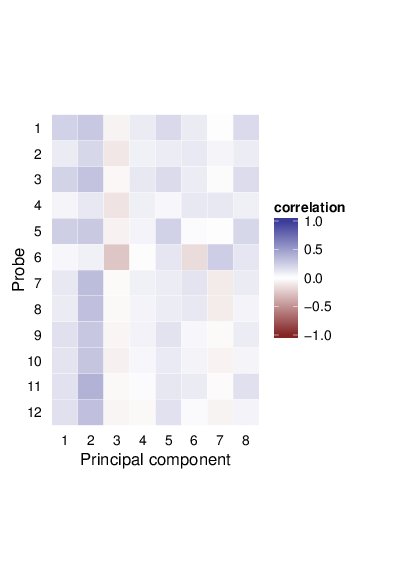
This section examines the methylation values of the dataset for quality-associated batch effects.
The heatmaps below visualize the Pearson correlation coefficients between the principal components and the signal levels of selected quality control probes.
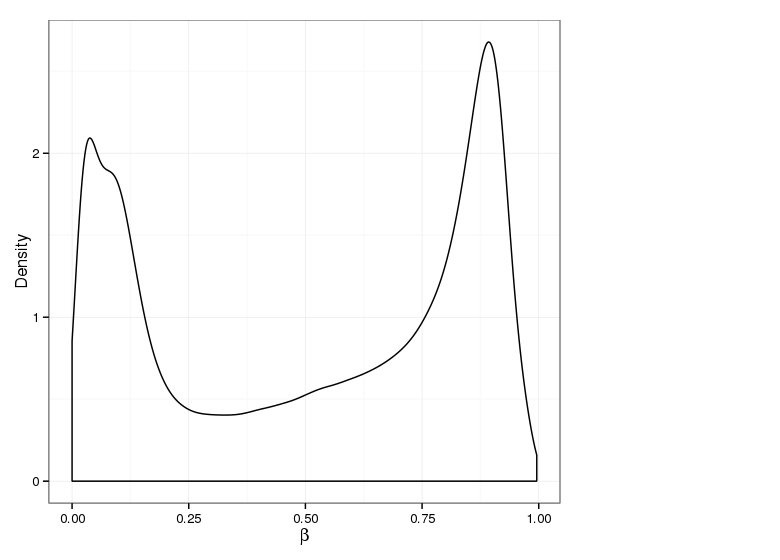
Methylation value distributions were assessed based on selected sample groups. This was done on probe and region levels. This section contains the generated density plots.
Methylation Value Densities of Sample Groups
The plots below compare the distributions of methylation values in different sample groups, as defined by the traits listed above.
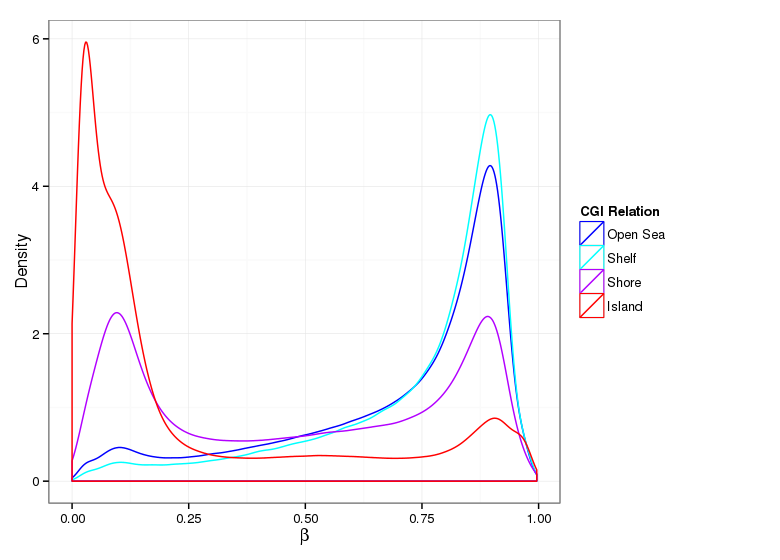
Methylation Value Densities of Probe Categories
In a similar fashion, the plot below compares the distributions of beta values in different probe types.
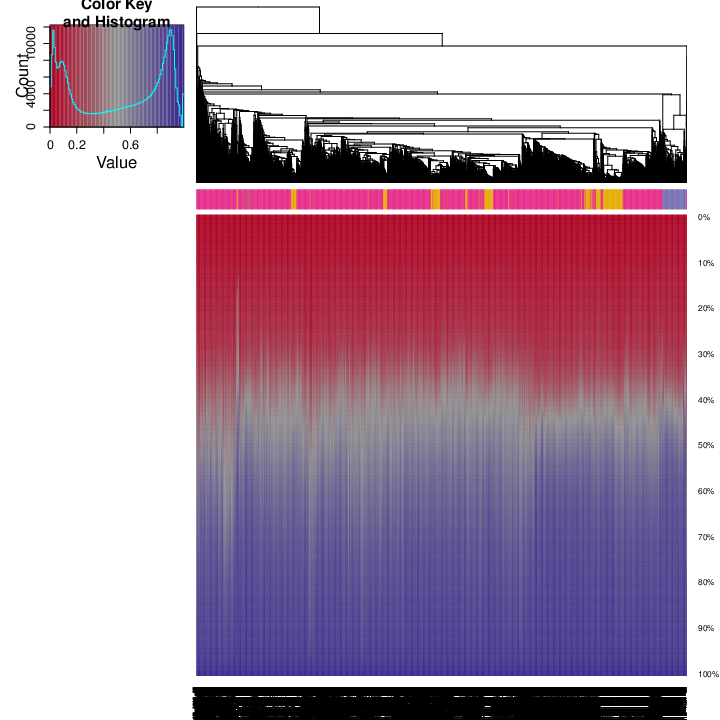
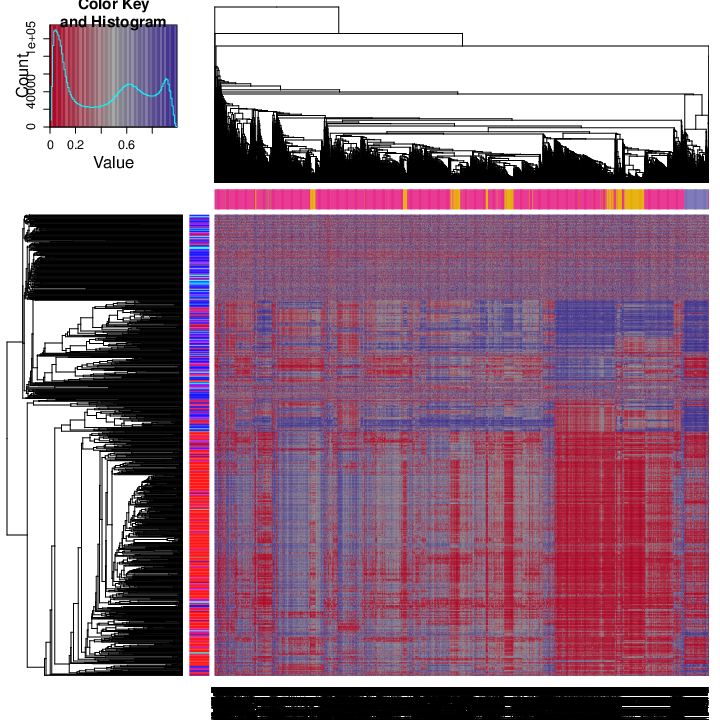
The figure below shows clustering of samples using several algorithms and distance metrics.
Identified Clusters
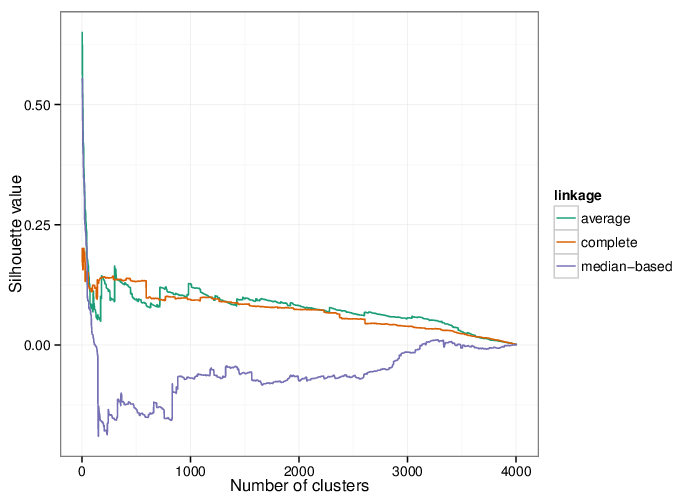
Using the average silhouette value as a measure of cluster assignment [1], it is possible to infer the number of clusters produced by each of the studied methods. The figure below shows the corresponding mean silhouette value for every observed separation into clusters.
The table below summarizes the number of clusters identified by the algorithms.
Clusters and Traits
The figure below shows associations between clusterings and the examined traits. Associations are quantified using the adjusted Rand index [2]. Rand indices near 1 indicate high agreement while values close to -1 indicate seperation. The full table of all computed indices is stored in the following comma separated files: