Exploratory Analysis

The table below lists the options of the executed module.

The specified traits were tested based on criteria for defining sample groups. The table below summarizes these traits.

In addition to CpG sites, there are 4 sets of genomic regions to be covered in the analysis. The table below gives a summary of these annotations.

Region length distributions

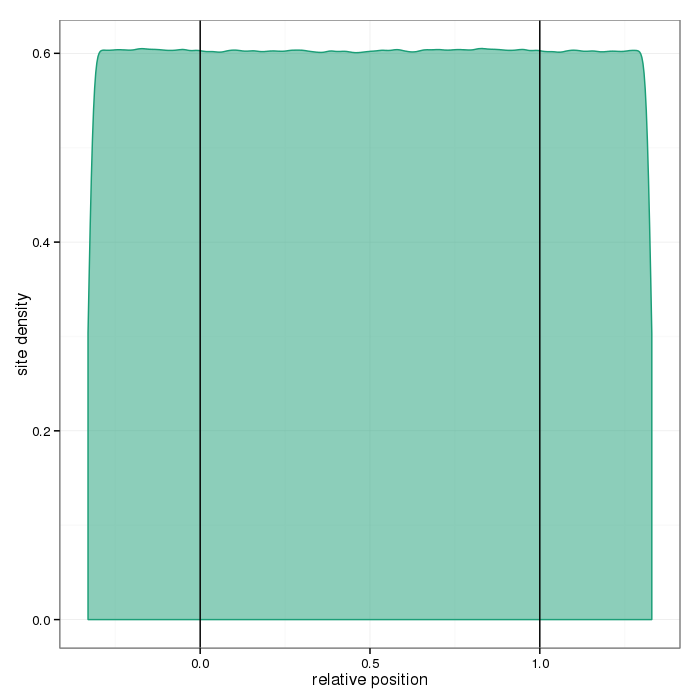
The plots below show region size distributions for the region types above.

Region type

tiling genes promoters cpgislands

Figure 1

Distribution of region lengths

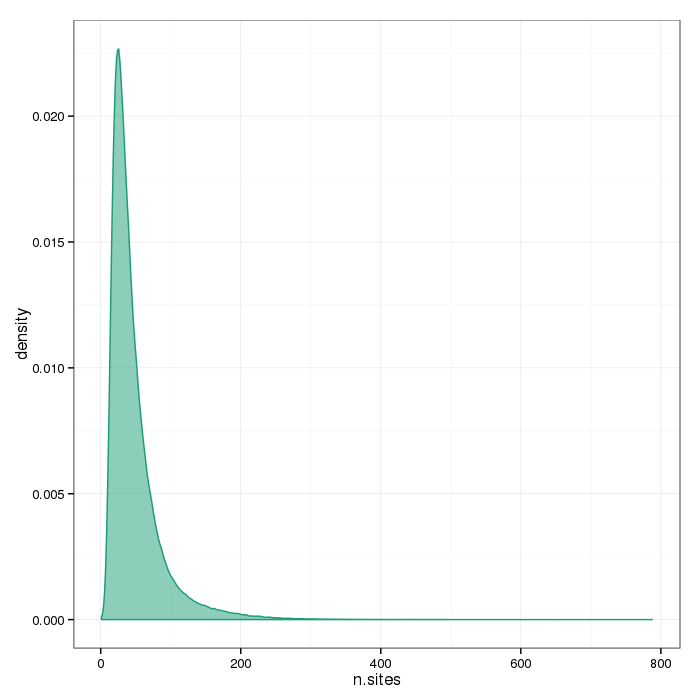
Number of sites per region

The plots below show the distributions of the number of sites per region type.

Region type

tiling genes promoters cpgislands

Figure 2

Distribution of the number of sites per region

Region site distributions

The plots below show distributions of sites across the different region types.

Region type

tiling genes promoters cpgislands

Figure 3

Distribution of sites across regions. relative coordinates of 0 and 1 corresponds to the start and end coordinates of that region respectively. Coordinates smaller than 0 and greater than 1 denote flanking regions normalized by region length.

Dimension reduction is used to visually inspect the dataset for a strong signal in the methylation values that is related to samples' clinical or batch processing annotation. RnBeads implements two methods for dimension reduction - principal component analysis (PCA) and multidimensional scaling (MDS).

One or more of the methylation matrices was augmented before applying the dimension reduction techniques because it contains missing values. The column Missing lists the number of dimensions ignored due to missing values. In the case of MDS, dimensions are ignored only if they contain missing values for all samples. In contrast, sites or regions with missing values in any sample are ignored prior to PCA.

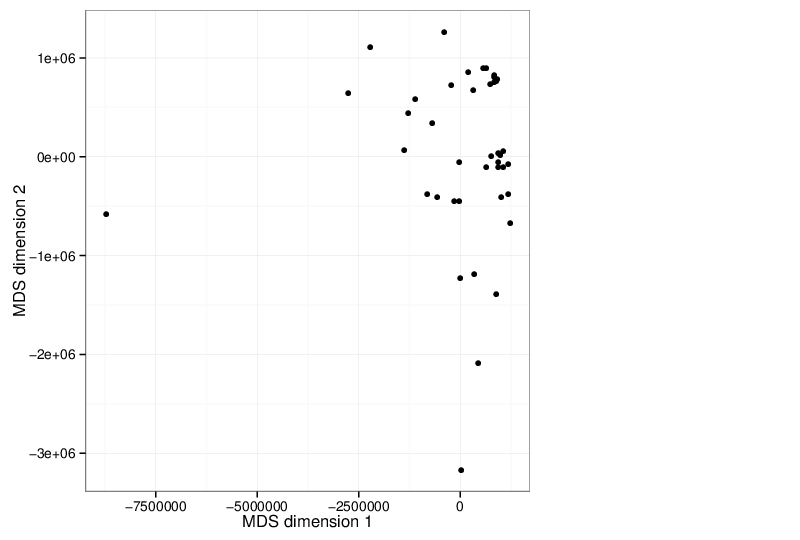
Multidimensional Scaling

The scatter plot below visualizes the samples transformed into a two-dimensional space using MDS.

Location type	sites tiling genes promoters cpgislands
Distance	Manhattan Euclidean
Sample representation	identifiers circles based on Source based on sample_class based on sample_cohort based on organ based on germ_layer
Sample color	black based on Source based on sample_class based on sample_cohort based on organ based on germ_layer

Figure 4

Scatter plot showing samples after performing Kruskal's non-metric mutidimensional scaling.

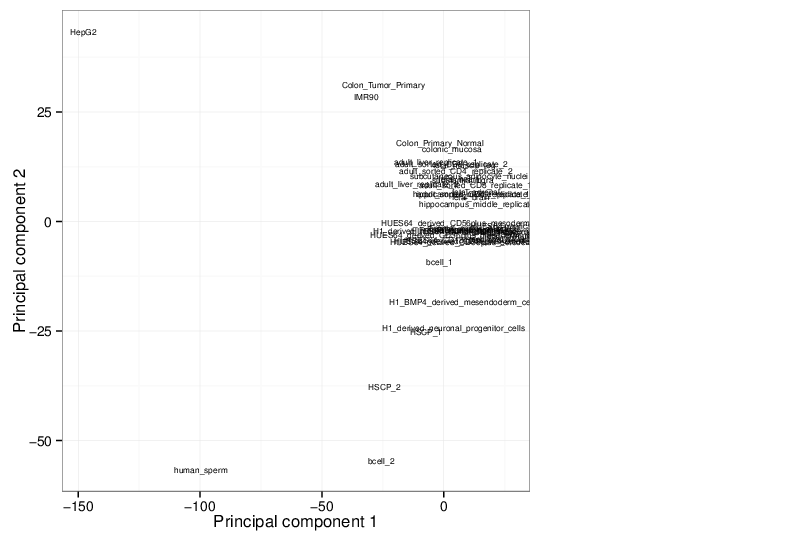
Principal Component Analysis

Similarly, the figure below shows the values of selected principal components in a scatter plot.

Location type	sites tiling genes promoters cpgislands
Principal components	first and second second and third
Sample representation	identifiers circles based on Source based on sample_class based on sample_cohort based on organ based on germ_layer
Sample color	black based on Source based on sample_class based on sample_cohort based on organ based on germ_layer

Figure 5

Scatter plot showing the samples' coordinates on principal components.

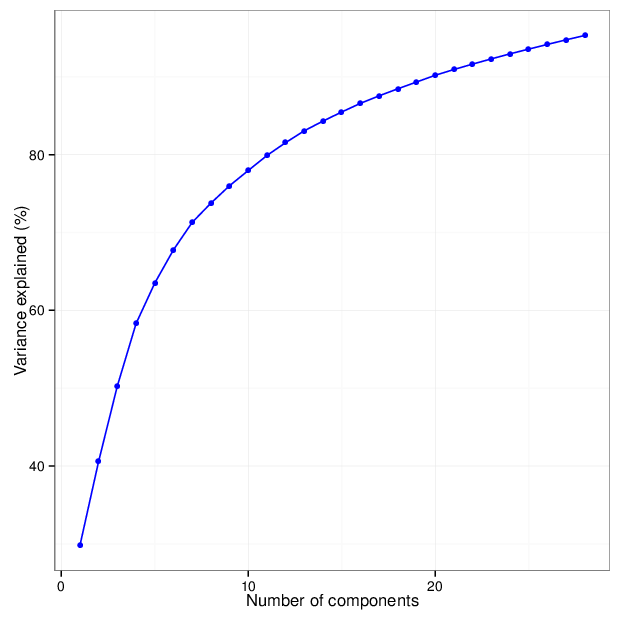
The figure below shows the cumulative distribution functions of variance explained by the principal components.

Location type

sites tiling genes promoters cpgislands

Figure 6

Cumulative distribution function of percentange of variance explained.

The table below gives for each location type a number of principal components that explain at least 95 percent of the total variance. The full tables of variances explained by all components are available in comma-separated values files accompanying this report.

Location Type	Number of Components	Full Table File
sites	28	csv
tiling	12	csv
genes	13	csv
promoters	14	csv
cpgislands	15	csv

In this section, different properties of the dataset are tested for significant associations. The properties can include sample coordinates in the principal component space, phenotype traits and intensities of control probes. The tests used to calculate a p-value given two properties depend on the essence of the data:

• If both properties contain categorical data (e.g. tissue type and sample processing date), the test of choice is a two-sided Fisher's exact test.
• If both properties contain numerical data (e.g. coordinates in the first principal component and age of individual), the correlation coefficient between the traits is computed. A p-value is estimated using permutation tests with 10000 permutations.
• If property A is categorical and property B contains numeric data, p-value for association is calculated by comparing the values of B for the different categories in A. The test of choice is a two-sided Wilcoxon rank sum test (when A defines two categories) or a Kruskal-Wallis one-way analysis of variance (when A separates the samples into three or more categories).

Note that the p-values presented in this report are not corrected for multiple testing.

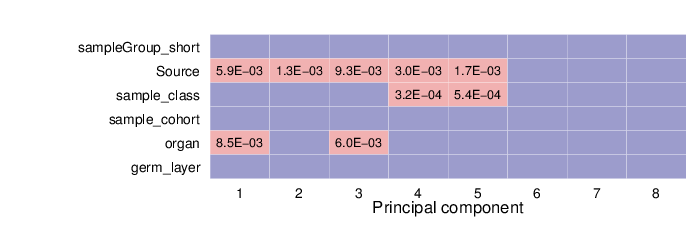
Associations between Principal Components and Traits

The computed sample coordinates in the principal component space were tested for association with the specified traits. Below is a list of the traits and the tests performed.

Trait	Test
sampleGroup_short	Kruskal-Wallis
Source	Kruskal-Wallis
sample_class	Kruskal-Wallis
sample_cohort	Kruskal-Wallis
organ	Kruskal-Wallis
germ_layer	Kruskal-Wallis

The heatmap below summarizes the results of permutation tests performed for associations. Significant p-values (values less than 0.01) are displayed in pink background.

Region type

sites tiling genes promoters cpgislands

Figure 7

Heatmap presenting a table of p-values. Significant p-values (less than 0.01) are printed in pink boxes. Non-significant values are represented by blue boxes. Bright grey cells, if present, denote missing values.

The full tables of p-values for each location type are available in CSV (comma-separated value) files below.

Location Type	File Name
sites	csv
tiling	csv
genes	csv
promoters	csv
cpgislands	csv

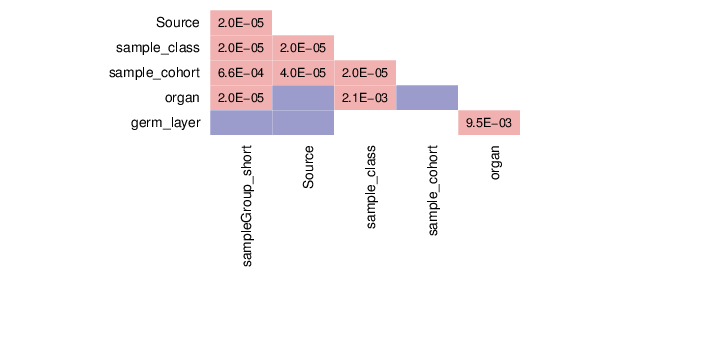
Associations between Traits

This section summarizes the associations between pairs of traits.

The figure below visualizes the tests that were performed on trait pairs based on the description provided above. In some cases, pairs of traits could not be tested for associations. These scenarios are marked by grey shapes, and the underlying reason is given in the figure legend. In addition, the calculated p-values for associations between traits are shown. Significant p-values (values less than 0.01) are displayed in pink background. The full table of p-values is available in a dedicated file that accompanies this report.

Heatmap of

tests performed p-values

Figure 8

(1) Table of performed tests on pairs of traits. Test names (Correlation + permutation test, Fisher's exact test, Wilcoxon rank sum test and/or Kruskal-Wallis one-way analysis of variance) are color-coded according to the legend given above.
(2) Table of resulting p-values from the performed tests on pairs of traits. Significant p-values (less than 0.01) are printed in pink boxes Non-significant values are represented by blue boxes. White cells, if present, denote missing values.

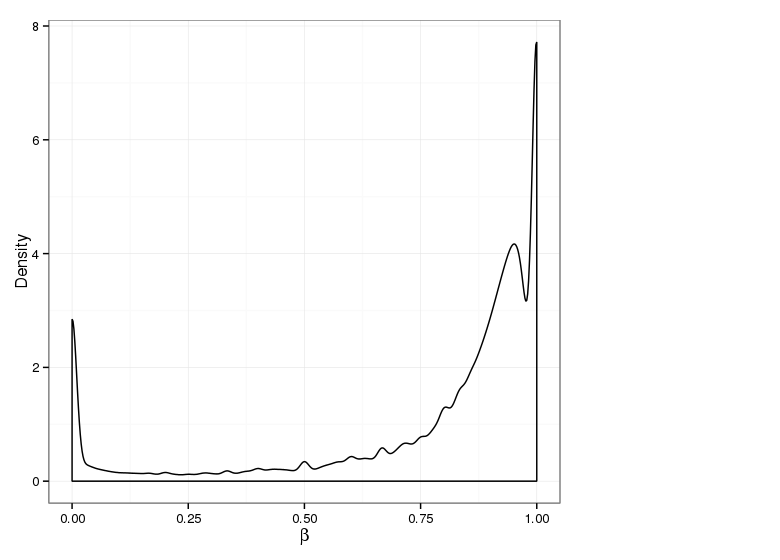
Methylation value distributions were assessed based on selected sample groups. This was done on site and region levels. This section contains the generated density plots.

Methylation Value Densities of Sample Groups

The plots below compare the distributions of methylation values in different sample groups, as defined by the traits listed above.

Sample trait	all samples Source sample_class sample_cohort organ germ_layer
Methylation of	sites tiling genes promoters cpgislands

Figure 9

Beta value density estimation according to sample grouping.

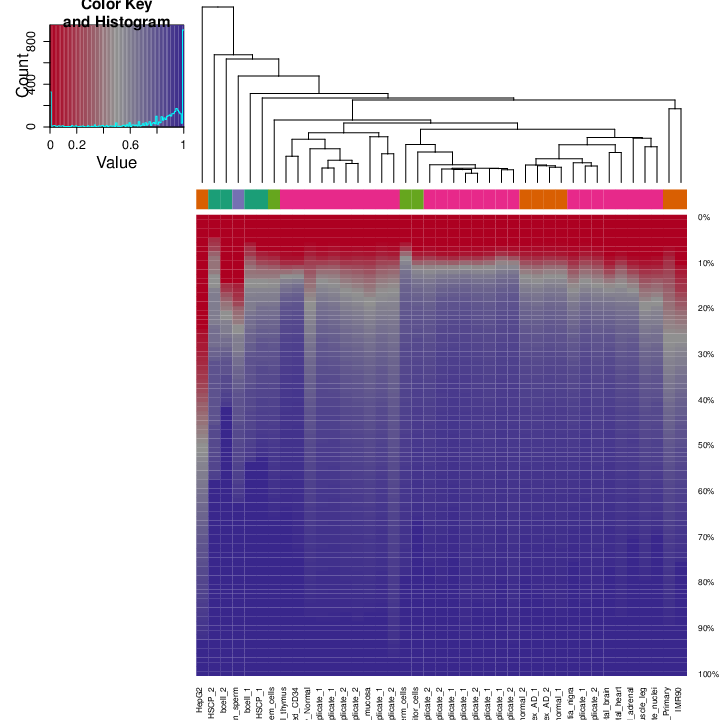
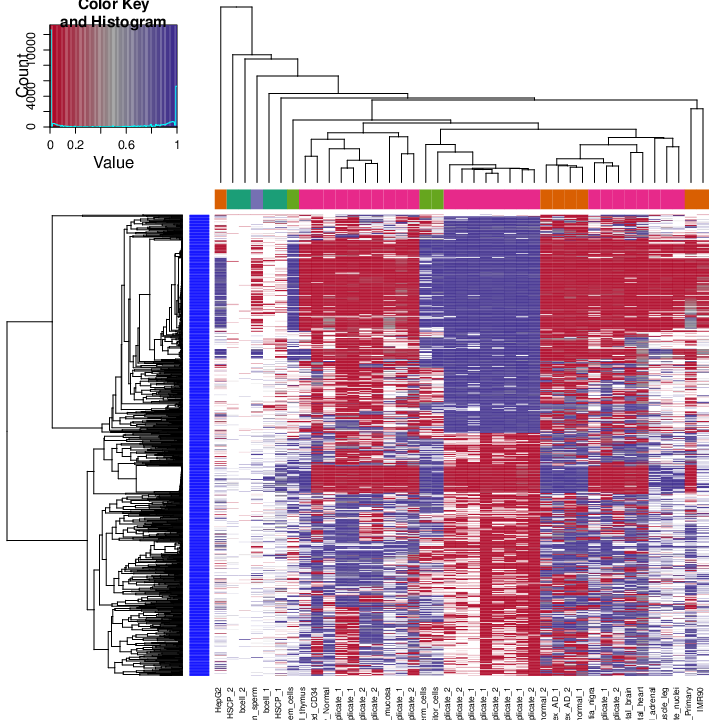
The figure below shows clustering of samples using several algorithms and distance metrics.

Site/region level	sites tiling genes promoters cpgislands
Dissimilarity metric	correlation-based Manhattan distance Euclidean distance
Agglomeration strategy (linkage)	average complete median-based
Sample color based on	Source sample_class sample_cohort organ germ_layer

Figure 10

Hierarchical clustering of samples based on all methylation values. The heatmap displays methylation percentiles per sample. The legend for sample coloring can be found in the figure below.

Site/region level	sites tiling genes promoters cpgislands
Dissimilarity metric	correlation-based Manhattan distance Euclidean distance
Agglomeration strategy (linkage)	average complete median-based
Sample color based on	Source sample_class sample_cohort organ germ_layer
Site/region color based on	CGI Relation CpG Density
Visualize	1000 most variable loci

Figure 11

Hierarchical clustering of samples based on all methylation values. The heatmap displays only selected sites/regions with the highest variance across all samples. The legend for locus and sample coloring can be found in the figure below.

Site/region level	sites tiling genes promoters cpgislands
Sample color based on	Source sample_class sample_cohort organ germ_layer
Site/region color based on	CGI Relation CpG Density

Figure 12

Probe and sample colors used in the heatmaps in the previous figures.

Identified Clusters

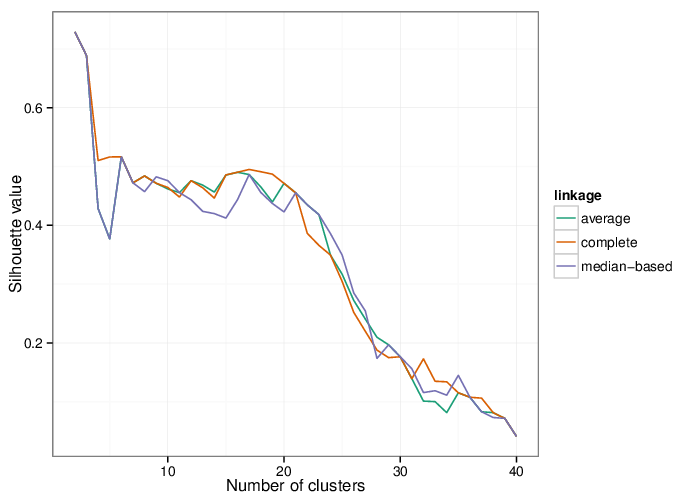
Using the average silhouette value as a measure of cluster assignment [1], it is possible to infer the number of clusters produced by each of the studied methods. The figure below shows the corresponding mean silhouette value for every observed separation into clusters.

Site/region level	cpgislands
Dissimilarity metric	correlation-based Manhattan distance Euclidean distance

Figure 13

Line plot visualizing mean silhouette values of the clustering algorithm outcomes for each applicable value of K (number of clusters).

The table below summarizes the number of clusters identified by the algorithms.

Site/region level

sites tiling genes promoters cpgislands

Metric	Algorithm	Clusters
correlation-based	hierarchical (average linkage)	2
correlation-based	hierarchical (complete linkage)	2
correlation-based	hierarchical (median linkage)	2
Manhattan distance	hierarchical (average linkage)	2
Manhattan distance	hierarchical (complete linkage)	2
Manhattan distance	hierarchical (median linkage)	2
Euclidean distance	hierarchical (average linkage)	2
Euclidean distance	hierarchical (complete linkage)	2
Euclidean distance	hierarchical (median linkage)	2

Metric	Algorithm	Clusters
correlation-based	hierarchical (average linkage)	2
correlation-based	hierarchical (complete linkage)	2
correlation-based	hierarchical (median linkage)	2
Manhattan distance	hierarchical (average linkage)	2
Manhattan distance	hierarchical (complete linkage)	2
Manhattan distance	hierarchical (median linkage)	2
Euclidean distance	hierarchical (average linkage)	2
Euclidean distance	hierarchical (complete linkage)	2
Euclidean distance	hierarchical (median linkage)	2

Metric	Algorithm	Clusters
correlation-based	hierarchical (average linkage)	2
correlation-based	hierarchical (complete linkage)	2
correlation-based	hierarchical (median linkage)	2
Manhattan distance	hierarchical (average linkage)	2
Manhattan distance	hierarchical (complete linkage)	2
Manhattan distance	hierarchical (median linkage)	2
Euclidean distance	hierarchical (average linkage)	2
Euclidean distance	hierarchical (complete linkage)	2
Euclidean distance	hierarchical (median linkage)	2

Metric	Algorithm	Clusters
correlation-based	hierarchical (average linkage)	2
correlation-based	hierarchical (complete linkage)	2
correlation-based	hierarchical (median linkage)	2
Manhattan distance	hierarchical (average linkage)	2
Manhattan distance	hierarchical (complete linkage)	2
Manhattan distance	hierarchical (median linkage)	2
Euclidean distance	hierarchical (average linkage)	2
Euclidean distance	hierarchical (complete linkage)	2
Euclidean distance	hierarchical (median linkage)	2

Metric	Algorithm	Clusters
correlation-based	hierarchical (average linkage)	2
correlation-based	hierarchical (complete linkage)	2
correlation-based	hierarchical (median linkage)	2
Manhattan distance	hierarchical (average linkage)	2
Manhattan distance	hierarchical (complete linkage)	2
Manhattan distance	hierarchical (median linkage)	2
Euclidean distance	hierarchical (average linkage)	2
Euclidean distance	hierarchical (complete linkage)	2
Euclidean distance	hierarchical (median linkage)	2

Clusters and Traits

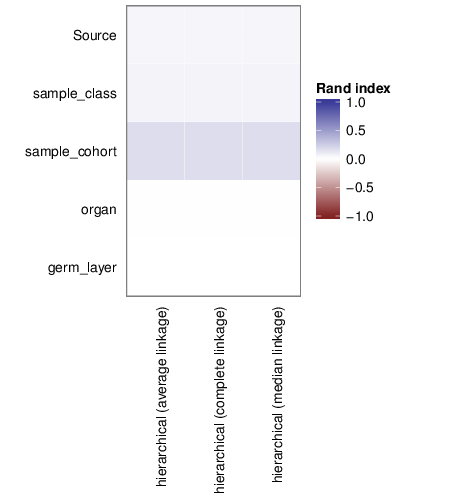
The figure below shows associations between clusterings and the examined traits. Associations are quantified using the adjusted Rand index [2]. Rand indices near 1 indicate high agreement while values close to -1 indicate seperation. The full table of all computed indices is stored in the following comma separated files:

• sites (csv)
• tiling (csv)
• genes (csv)
• promoters (csv)
• cpgislands (csv)

Site/region level	sites tiling genes promoters cpgislands
Dissimilarity metric	correlation-based Manhattan distance Euclidean distance

Figure 14

Heatmap visualizing Rand indices computed between sample traits (rows) and clustering algorithm outcomes (columns).

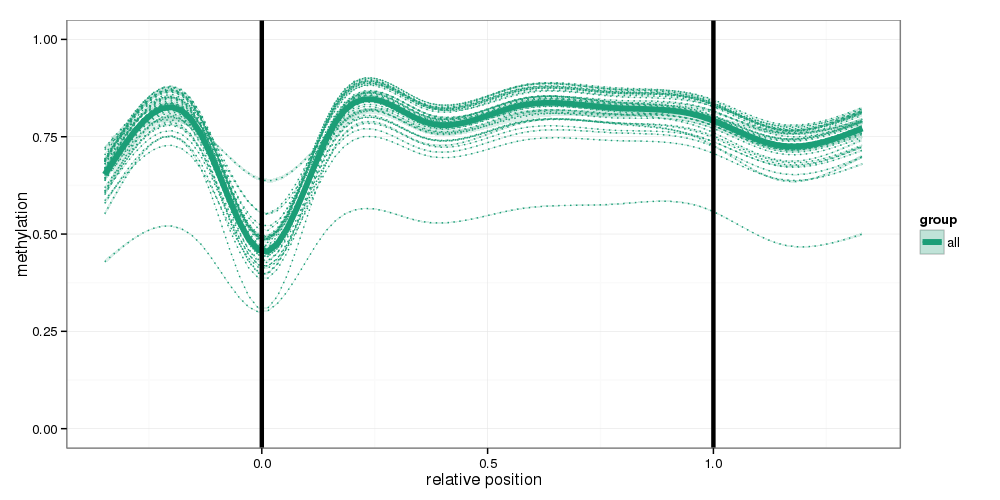
Methylation profiles were computed for the specified region types. Composite plots are shown

Region type	genes promoters
Sample trait	all samples Source sample_class sample_cohort organ germ_layer

Figure 15

Regional methylation profiles (composite plots) according to sample groups. For each region in the corresponding region type, relative coordinates of 0 and 1 corresponds to the start and end coordinates of that region respectively. Coordinates smaller than 0 and greater than 1 denote flanking regions normalized by region length. Scatterplot smoothers for each sample and sample group were fit. Horizontal lines indicate region boundaries. For smoothing, generalized additive models with cubic spine smoothing were used. Deviation bands indicate 95% confidence intervals

1. Rousseeuw, P. J. (1987) Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53-65
2. Hubert, L. and Arabie, P. (1985) Comparing partitions. Journal of Classification, 2(1), 193-218